Spectral enhancement
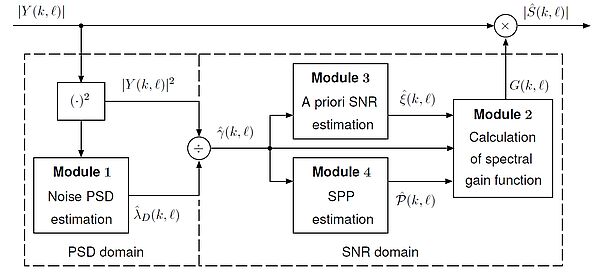
All techniques processing in the SNR domain have a decisive impact on the properties of the spectral gain function applied to denoise the noisy speech and consequently on the quality of the denoising procedure. Thus, a finding of an optimal spectral gain function with better trade-off between high noise suppression and low speech distortion is still a currect topic of ongoing research.
Three modules of spectral enhancement
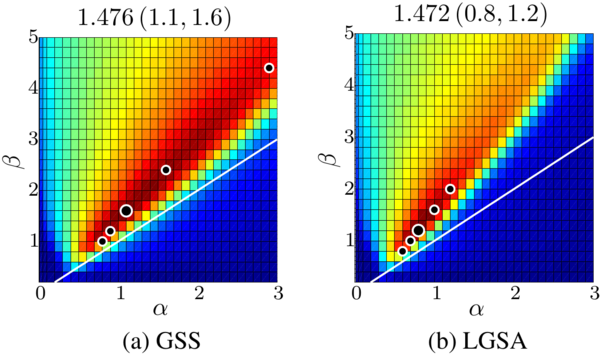
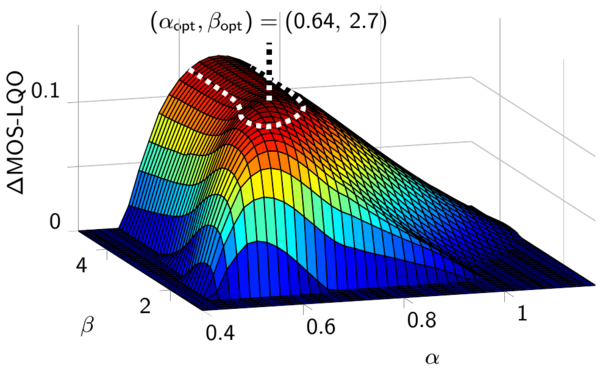
Starting with the seminal paper Boll (1979) introducing the spectral subtraction algorithm for noise suppression of short-time spectral amplitudes of noisy speech signal much research has been devoted to find an optimal gain function. For this, a trade-off between high noise suppression and low speech distortion available in a denoised speech signal has to be solved and a so called musical noise has to be avoided. Thus the minimum mean squared error (MMSE) of log-spectral amplitude (LSA) estimator was shown to successfully reduce the musical noise phenomenon. However a closer look at the shapes of the MMSE-LSA gain curves revealed that the price to pay for the good quality of the enhanced speech signals was a weaker noise suppression in regions with low speech energy. Further it was proposed to carry out the enhancement in domains other than the magnitude or power spectral domain. The MMSE-based generalized spectral subtraction (GSS) gain functions proposed by Sim (1998) were derived, e.g., in the domain of the spectral amplitudes raised to a generalized power exponent, whose value 1 and 2 correspond to the magnitude and the power spectral domain, respectively. Investigations have shown that the MMSE-GSS constrained parametric estimator results in a respectable ability to suppress noise however on costs of speech quality.
Thus, a finding of an optimal spectral gain function with better trade-off between high noise suppression and low speech distortion is still a currect topic of ongoing research.
While the a posteriori SNR calculated from the noise PSD estimates is considered as a correction parameter of the gain function, the a priori SNR has been advised to be used as its dominant parameter. A priori SNR is usually calculated from the a posteriori SNR by using the well-known decision directed (DD) approach as a weighted sum of two terms. The first is the a priori SNR estimate calculated from the spectral magnitude of the enhanced speech signal of the previous frame, and the second is the maximum likelihood (ML) estimate of the a priori SNR based on the current a posteriori SNR estimate. Thus, the a priori SNR estimation exploits information of both the noise PSD tracker and the used gain function, and it can be considered a central component of a spectral enhancement system. However, the DD approach suffers from one well known drawback - slow response to an abrupt change in the instantaneous SNR known also as the reverberation effect. To overcome this shortcoming novel approaches are developed in our department.
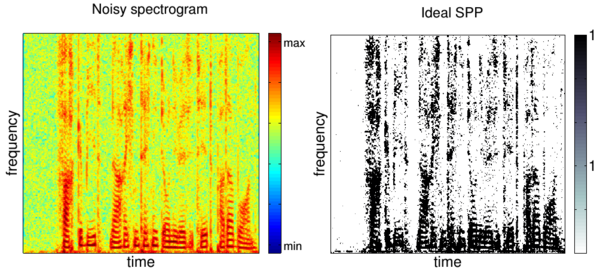
The estimation of the SPP for each individual time-frequency slot is a important part of many speech processing systems. Thus, the widespread speech enhancement approaches based on estimation of the short-time spectral amplitude of the clean speech signal crucially depend on an SPP estimator. However, a reliable SPP estimator is difficult to obtain in a noisy scenario. It is well known that speech signals have characteristic temporal and spectral correlations in the time-frequency domain. Usually, this fact is exploited by smoothing the estimated characteristics, such as the SPP estimations themselves, the a priori SNR, or even the gain factor of individual time-frequency slot across time, frequency, or both. However rather than smoothing the estimates with heuristically chosen filter parameters in a postprocessing step, the correlations can be directly employed in the estimation of the SPP by applying a statistical inference on the a posteriori SNR estimates averaged over a certain adjacent time-frequency slots. Developing of SPP estimators, which are able to take into account spectral correlations in the neighbouring time-frequency slots, has a high priority in our group.